Not an expert but I have a little bit of knowledge, so here’s my take:
The 2 parameter model works exactly as you would expect - take any point on the curve, take off your FTP and divide by the time in seconds gives you W’. The trouble with that model is that you can’t actually produce the power it thinks you can at very short durations: 10 seconds at 2816 Watts! No chance.
This model assumes that when you deplete W’ at any given power output, you will be unable to continue pedelling which is only correct in one sense: you can’t continue to pedal at that particular intensity.
Now, I’m not particularly familiar with the 3 parameter model, which, as you described, does not follow the same pattern.
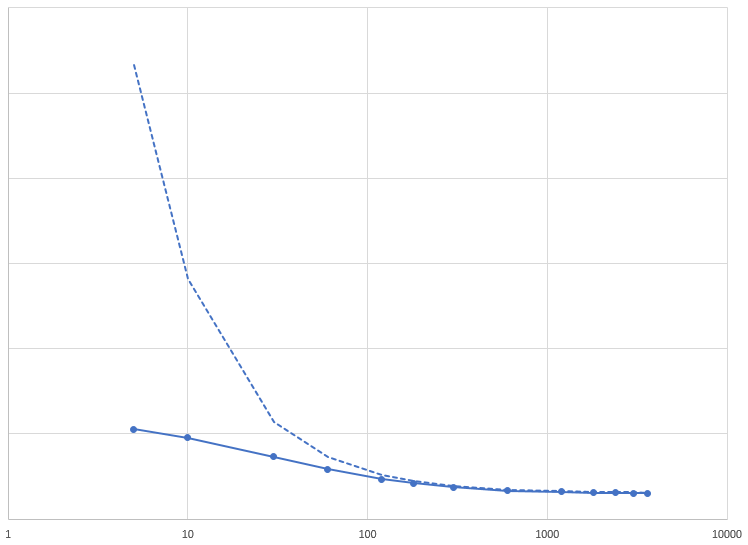
Here is a comparison between the actual power curve and the constant work above FTP curve:
They start diverging significantly once you get down to about 180 seconds. It makes intuative sense that you could never output a wattage of 25000 for a single second or 5000 for 5 seconds etc so there is some sort of degradation of W’ in the very short durations.
Less obviously, there is also a reduction in W’ even much further along the curve which isn’t so intuative.
Above I referred to not being able to continue pedalling at the same intensity once you hit the point on the model curve (assuming it is correct), but that doesn’t mean you can’t continue to pedal above FTP, it just means that your ability to continue producing, say 400 Watts is compromised. This is due to being not only being limited by the amount of energy that you can use, but also by the rate that you can use it. In this case you get to a point where you can no longer produce 400 Watts, but can continue to produce 399, 398, 397 etc for a few seconds each until you finally get down to your threshold. This energy is also part of W’ but can never be represented on the power duration curve because it’s imposible to deplete it fully at a single intensity.
Now, I must admit that my knowledge of this comes from learning about Xert and that may well be different to Morton’s model in the exact detail (no doubt it is) but it shows exactly the same sort of ‘behaviour’.
Mike
 But, there are more;
But, there are more; 