Freewheeling at 0W is just an extreme example to show the formula is wrong.
Low level efforts got a bonus from being in the same workout as high level efforts as well which causes long rides to have inflated TSS.
If you go downhill you don’t need another 10m, maybe 1m. so your TSS won’t be so high as in your first post.
Just try it. So, in reality that is not a real problem, more a problem ‚on paper‘.
It doesn’t take a minute to ride down from the hill you need 10m to climb either. Just today I’ve done a climb and then rode it down at the end of the workout. It took me 52m to go up and 18 minutes to go down even though I wasn’t actually freewheeling and got a very good downhill time (in the top 10% overall on a segment world tour pros use all the time on their camps on Tenerife). Freewheeling it would take 24 minutes or so (I know because I was riding it with a friend who doesn’t usually ride in the mountains). KOMs are: downhill 14:14, uphill 30:18, again set by World Tour pros.
The formula is not perfect, but there is no better. What would be your better Load calculation?
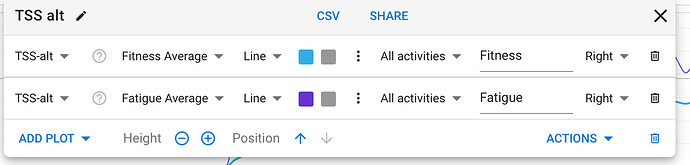
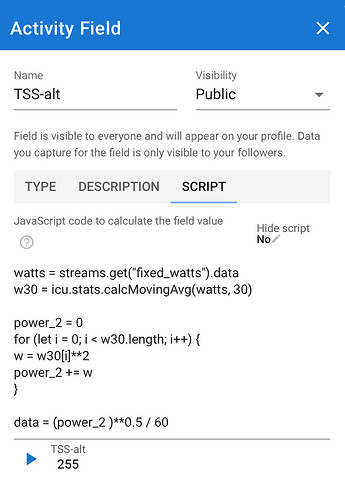
Let me repeat a better formula:
[EDITED after @R2Tom pointed my mistake]
1)Calculate rolling 30 seconds average function of power expressed as % of FTP just as in TSS
2)Square it
3)Calculate area under it
4)multiply by 100 to get TSS scale
You end up with the same TSS function but without artificially inflating zero/low efforts in workouts with some intensity in it.
The problem is that TSS increases linearly with time but NP squared (what you end up with from NP * IF) doesn’t linearly decrease. This means that inserting near zero/low efforts into the workout inflates their value. It’s not a problem only on paper either. Just today I’ve done 3x15 sub threshold intervals on otherwise quite spirited ride and got the same TSS score I’ve got on lazy ride 2 days ago just because that lazy ride was an hour longer, mainly because downhills on it were very technical and I needed to use breaks a lot while today I was descending at decent speed on good roads.
Another way would be to just slice the ride into many pieces, calculate TSS for all of them and then sum them up. It’s just integrating though so one can do that instead as it’s simpler to implement and more precise.
Let me bring your attention to this again:
Actually Intervals.icu does leave the pause out of the TSS calculation, it does that even if you don’t pause otherwise rides with punctures and coffee stops get inflated TSS. TSS of 151 for 4h30 doesn’t seem high. The time in zones info is incorrect. Intervals.icu uses “moving” to decide what to include there and this ride has no velocity or moving streams. I should be able to fix this because there is no data for that 90 min part.
Clearly the problem is obvious enough but deciding what to include based 0 efforts is just a very small part of it. Just to point to an obvious example: if it’s 1W-10W instead of a 0 it will not change anything and depending on the terrain you ride in you can get a lot of 1-10W time. That wouldn’t be a problem if you are in the mountains all the time but then you come back home and wonder why it’s so difficult to keep your fitness score high and end up overreaching/overtraining. Just take integral over a squared function, calclate square root of that and then everything makes sense (or at least allow users to use that function instead of original TSS). The math and the algorithm also becomes way easier and not arbitrary. No reason to decide what is and what isn’t a real pause either.
Again, it doesn’t alter underlying physiological assumptions. 2hours at 70% of FTP still results in the same score as 1hour at 100% of FTP. I am not here to discuss if it’s ideal or not. I don’t want to question underlying physiology or assumptions. I am here to correct the math side of it as it’s a clear problem with an elegant solution.